13.3 Problem Solving: Recursive Mathematical Functions

Many mathematical functions are defined recursively. An example is the factorial of a number n (n!).

0! is 1.
n! is n × (n - 1)!, for n > 0.

Thus, 4! is 4 × 3 × 2 × 1, or 24. It is quite easy to implement this definition as a recursive function in Ada.

Example 13.2

Function Factorial in Program 13.3 computes the factorial of its argument N.

Program 13.3
Recursive Factorial Function

FUNCTION Factorial (N : IN Natural) RETURN Positive IS
-- Computes the factorial of N (N!) recursively
-- Pre : N is defined and N >= 0
-- Post: returns N!
  
BEGIN  -- Factorial   

  IF N = 0 THEN
    RETURN 1;                   -- stopping case   
  ELSE
    RETURN N * Factorial(N-1);  -- recursion   
  END  IF;

END Factorial;

The recursive step

    Result := N * Factorial(N-1);

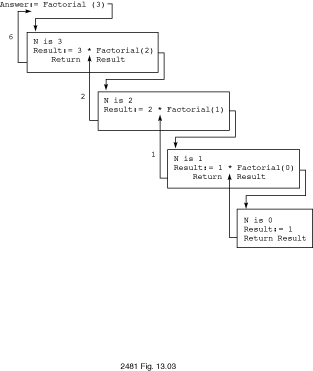
implements the second line of the factorial definition above. This means that the result of the current call (argument N) is determined by multiplying the result of the next call (argument N-1) by N.

A trace of

    Answer := Factorial(N => 3);

is shown in Figure 13.3.

Figure 13.3
Trace of Answer := Factorial(3)

Figure 13.3

The value returned from the original call, Factorial(N => 3), is 6, and this value is assigned to Answer. Be careful when using the factorial function; its value increases very rapidly and could lead to an integer overflow exception (e.g., 10! is 24,320).

Although the recursive implementation of function Factorial follows naturally from its definition, this function can be implemented easily using iteration. The iterative version is shown in Program 13.4; it is in fact the same function that appeared back in Program 5.19, as one of the useful functions there.

Program 13.4
Factorial, Iterative Version

FUNCTION Factorial_Iterative (N : IN Natural) RETURN Positive IS
-- Computes the factorial of N (N!) iteratively
-- Pre : N is defined and N >= 0
-- Post: returns N!
  
  Result : Positive;                 -- holds the product

BEGIN  -- Factorial_Iterative   

  Result := 1;  
  FOR Count IN 2 .. N LOOP
    Result := Result * Count;
  END LOOP;

  RETURN Result;

END Factorial_Iterative;

Note that the iterative version contains a loop as its major control structure, whereas the recursive version contains an IF statement.

Example 13.3

The Fibonacci numbers are a sequence of numbers that have many varied uses. They were originally intended to model the growth of a rabbit colony. The Fibonacci sequence 1, 1, 2, 3, 5, 8, 13, 21, 34,... increases rapidly: Each number in the sequence is the sum of the two previous ones. The fifteenth number in the sequence is 610 (that's a lot of rabbits). The Fibonacci sequence is defined below.

Fib₁ is 1.
Fib₂ is 1.
Fib_n is Fib_n-2 + Fib_n-1, for n > 2.

Verify for yourself that the sequence of numbers shown above is correct. A recursive function that computes the Nth Fibonacci number is shown as Program 13.5. Although easy to write, the Fibonacci function can run rather slowly because each recursive step generates two recursive calls to function Fibonacci.

Program 13.5
Fibonacci

FUNCTION Fibonacci (N : IN Natural) RETURN Positive IS
-- Returns the Nth Fibonacci number, computed recursively
-- Pre : N is defined and N >= 0
-- Post: returns N!
  
BEGIN  -- Fibonacci   

  IF (N = 1) OR (N = 2) THEN
    RETURN 1;
  ELSE
    RETURN Fibonacci(N-2) + Fibonacci(N-1);
  END IF;

END Fibonacci;

Example 13.4

The greatest common divisor (GCD) of two positve integers is the largest integer that divides them both; Euclid's algorithm for finding the GCD is defined recursively as follows:

GCD(M, N) is N if N <= M and N divides M.
GCD(M, N) is GCD(N, M) if M < N.
GCD(M, N) is GCD(N, remainder of M divided by N) otherwise.

This algorithm states that the GCD is N if N is the smaller number and N divides M. If M is the smaller number, the GCD determination should be performed with the arguments transposed. If N does not divide M, the answer is obtained by finding the GCD of N and the remainder of M divided by N. The Ada function GCD is shown as Program 13.6.

Program 13.6
Greatest Common Divisor, Recursive Version

FUNCTION GCD (M, N : IN Positive) RETURN Positive IS
-- Pre : M and N are defined.
-- Post: Returns the greatest common divisor of M and N.

  Result: Positive;
   
BEGIN -- GCD   

  IF (N <= M) AND (M REM N = 0) THEN
    Result := N;
  ELSIF M < N THEN
    Result := GCD(N, M);
  ELSE
    Result := GCD(N, M REM N);
  END IF;

  RETURN Result;

END GCD;

Exercises for Section 13.3

Self-Check

If Ada did not have an exponentiation operation (**), we could write our own. Complete the following recursive function that calculates the value of a number (Base) raised to a power (Power).

FUNCTION PowerOf (Base: Integer; Power: Positive) RETURN Integer IS

  Result: Integer;

BEGIN -- PowerOf

  IF Power = ______ THEN
    Result := ________ ;
  ELSE
    Result := ________ * ________ ;
  END IF;

END PowerOf;

What is the output of the following program? What does function Strange compute?

WITH Ada.Text_IO;
WITH Ada.Integer_Text_IO;
PROCEDURE TestStrange IS
     
  FUNCTION Strange (N : Integer) RETURN Integer IS
    Result: Integer;
  BEGIN
    IF N = 1 THEN
      Result := 0;
    ELSE 
      Result := 1 + Strange (N / 2);
    END IF;
  END Strange;

BEGIN -- TestStrange

  Ada.Integer_Text_IO.Put(Item => Strange(8);
  Ada.Text_IO.New_Line;

END TestStrange;

Explain what would happen if the terminating condition for the Fibonacci function is just (N = 1).

Programming

Write a recursive function, FindSum, that calculates the sum of successive integers starting at 1 and ending at N (i.e., FindSum(N) = (1 + 2 + ... + (N - 1) + N)).
Write an iterative version of the Fibonacci function.